++ 50 ++ 正規分布 確率 例題 109517-正規分布 確率 例題

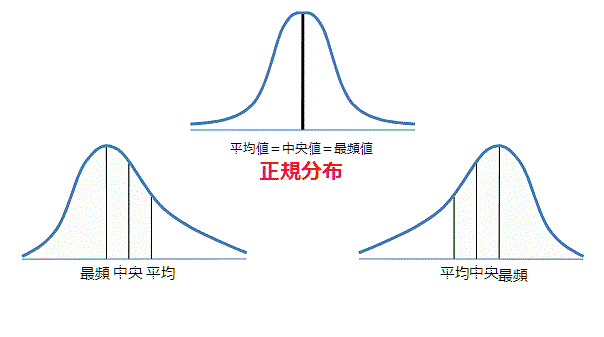
正規分布の分かりやすいまとめ Avilen Ai Trend

 例題1 表1で示された確率分布の内、以下の確率分布における期待値と分散を証明せよ。 (1) ベルヌーイ分布 (2) 二項分布 (3) 正規分布 ただし解答に当たり、下記2つの関係式を証明なしで誤差関数は，主に正規分布の累積分布関数 (CDF)を記述する際に用いられる特殊関数 (special function)の一種である．一般にCDFは，確率密度関数 (PDF)の定積分によって与えられるが，正規分布のPDFに対してはこの積分を解析的に実行することができない

正規分布 確率 例題

正規分布 確率 例題- 正規分布とは 正規分布とは、データが平均値付近に集まって、平均値を境に左右対称にばらついた分布です。 正規分布は、統計学において最も重要な確率分布の1つです。 なぜなら、多くの統計的手法は「データが正規分布に従うこと」が前提として考え確率値 p 正規分布表を用いた確率計算の例題 ：製品の品質管理 • テキスト61ページの例題5．1：「品質管理」 化粧品のボトル。工場でのボトル詰め工程により、実際 にボトル詰めされた製品の容量にはバラツキが生じて しまう。

正規分布から工程能力を理解する ひんぽの勉強机

 qc検定練習問題3級"正規分布（確率計算を含む）"① ※qc検定のおすすめ参考書と過去問題集はこちらで紹介しています。 問題1 正規分布に関する次の文書において、 内に入る適切なものを下欄の選択肢から一つ選びなさい。正規分布では（平均）±196×（標準偏差）の範囲に入る確率は95%になる．（ z=196 のときの正規分布表の値が 0475 だから両側で 095 になる．） ※ 標本平均 の標準偏差として利用するもの1 正規分布の利用例 では，今まで学習した正規分布を,面積と確率という事柄を意識しながら練習問題を解いていくことにしましょう。 例題1 確率変数 X が正規分布 N (4,32) にしたがうとき，次の確率を求めよ。 正規分布表呼び出し→ (1) P (4≦X≦6) (2) P (3≦

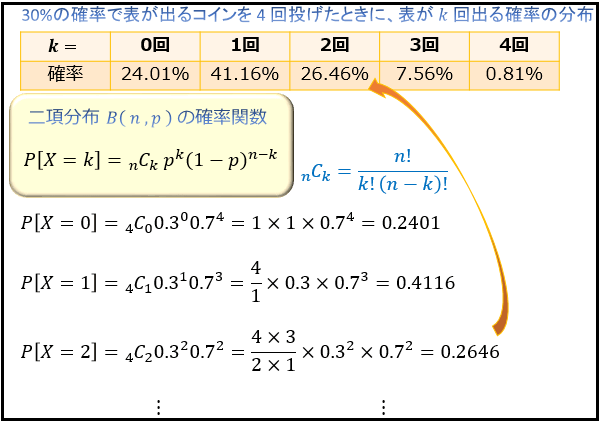
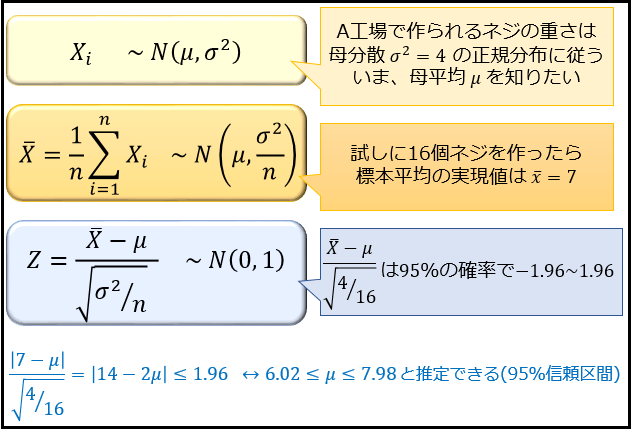
この例題では母集団が正規分布 に従うことを仮定している．したがっ て，標本平均 は正規分布 に従う 命題 ．つまり，確率密度 関数 に従う 式 ．このとき，標本平均 が の値をとる確率は， である 式 ． 母平均 に対して，次式を満たす定数 があったと 二項分布を正規分布で近似する定理について解説。 例題 公平なコインを回投げるとき，表が5100回以上出る確率を求めよ。 {x5000}{50} y = ⋅ 2 1 2 1 x − ⋅ 2 1 = 50 x − 5000 は近似的に標準正規分布に従う。 求める確率もくじ 1 二項分布は正規分布だけでなく、ポアソン分布にも近似できる 11 起こる確率が低いとき、ポアソン分布が利用される;

正規分布 確率 例題のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

Sec4	Sec4	Sec4
Sec4	Sec4	Sec4
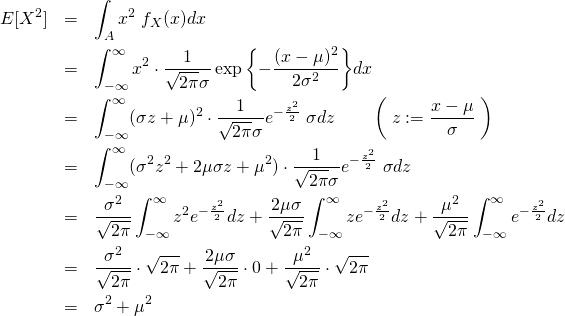Sec4	Sec4	Sec4
Sec4	Sec4	Sec4
Sec4	Sec4	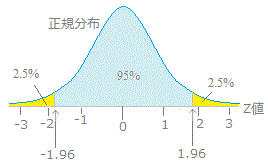Sec4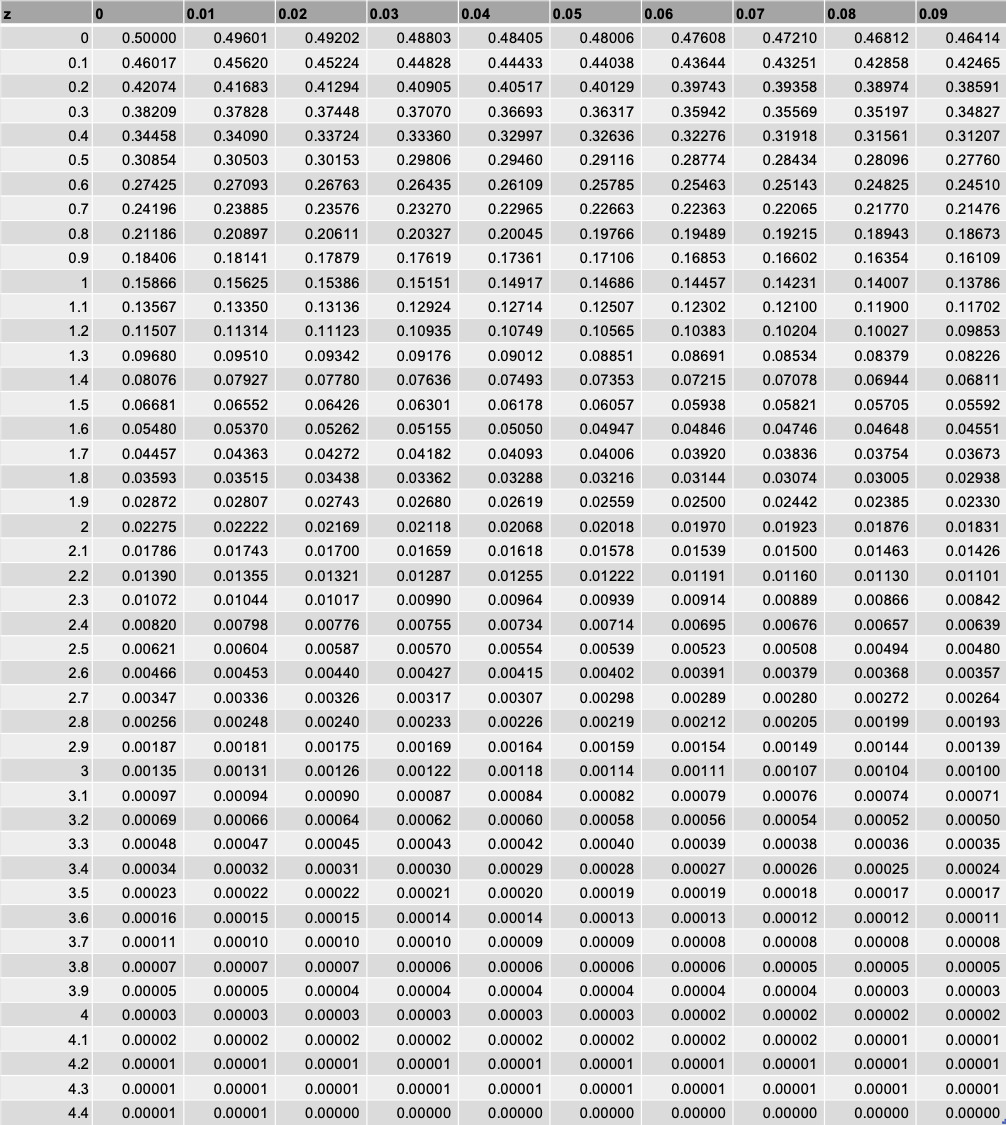
Sec4	Sec4	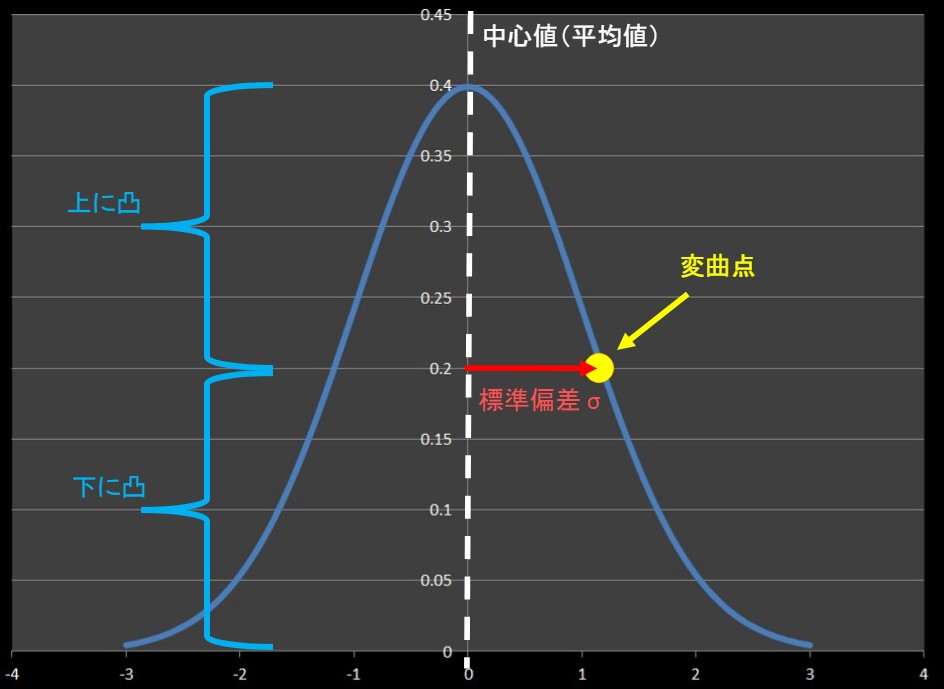Sec4
Sec4	Sec4	Sec4
Sec4	Sec4	Sec4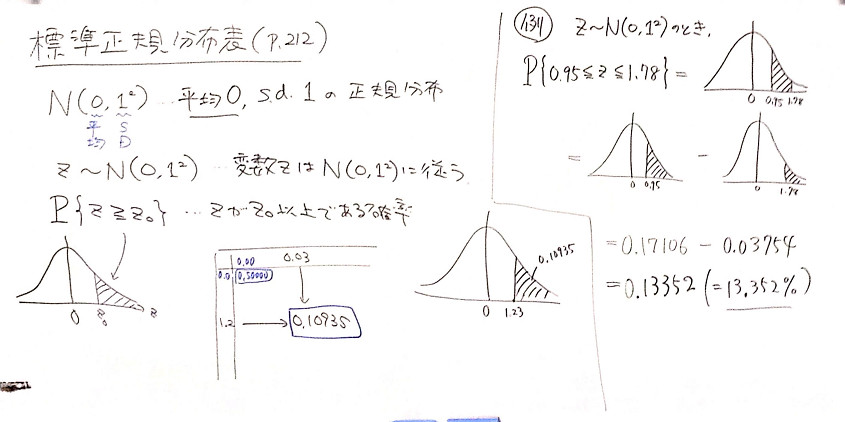
Sec4	Sec4	Sec4
Sec4	Sec4	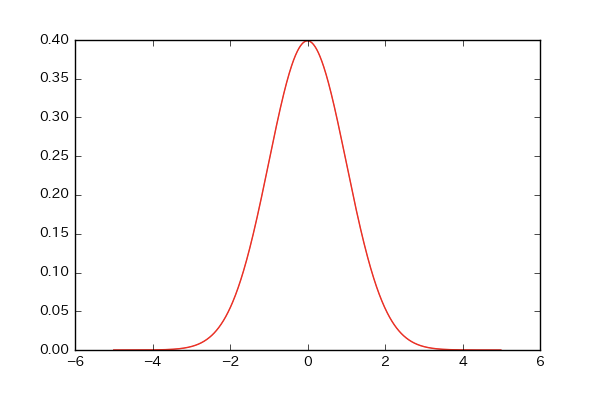Sec4
Sec4	Sec4	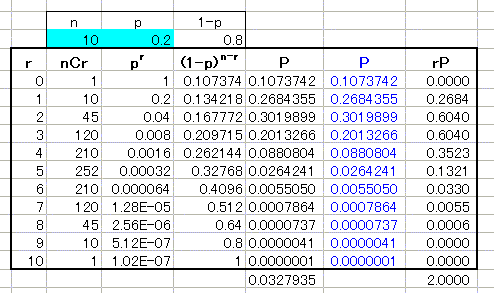Sec4
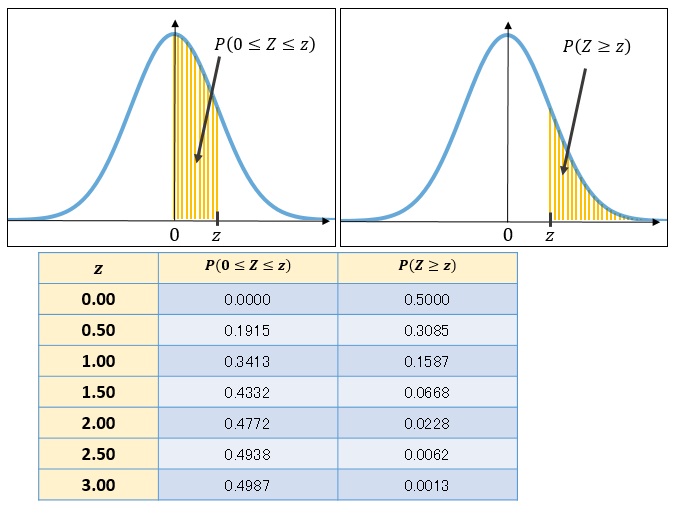Sec4	Sec4	Sec4
Sec4	Sec4	Sec4
Sec4	Sec4	Sec4
Sec4	Sec4	Sec4
Sec4	Sec4	Sec4
Sec4	Sec4	Sec4
Sec4	Sec4	Sec4
Sec4	Sec4	Sec4
Sec4	Sec4	Sec4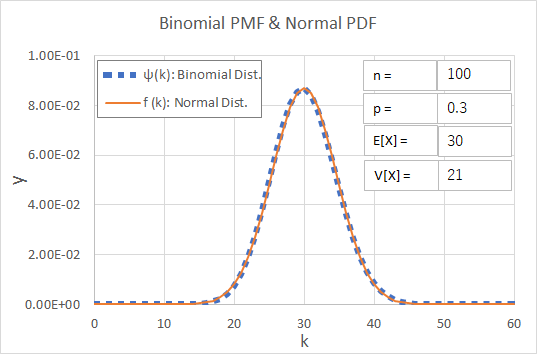
Sec4	Sec4	Sec4
Sec4	Sec4	Sec4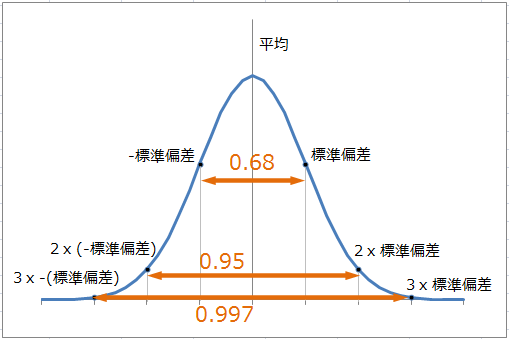
Sec4	Sec4	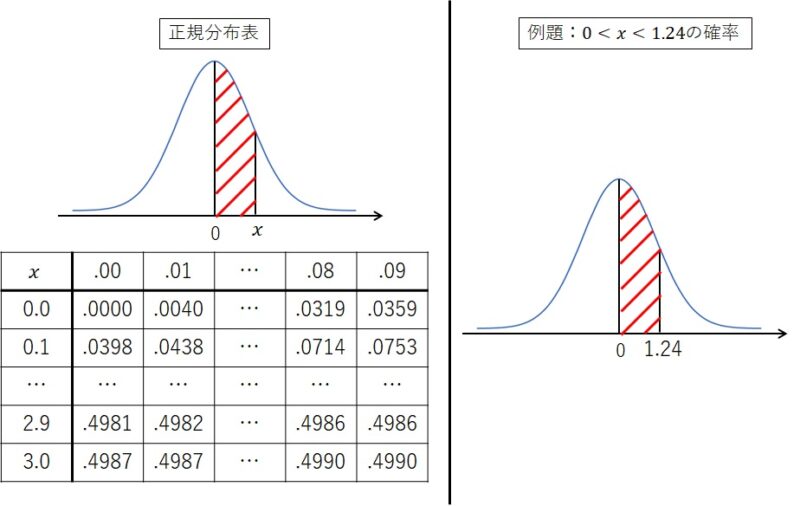Sec4
Sec4	Sec4	Sec4
Sec4	Sec4	Sec4
Sec4	Sec4	Sec4
Sec4	Sec4	Sec4
Sec4	Sec4	Sec4
Sec4	Sec4	Sec4
Sec4	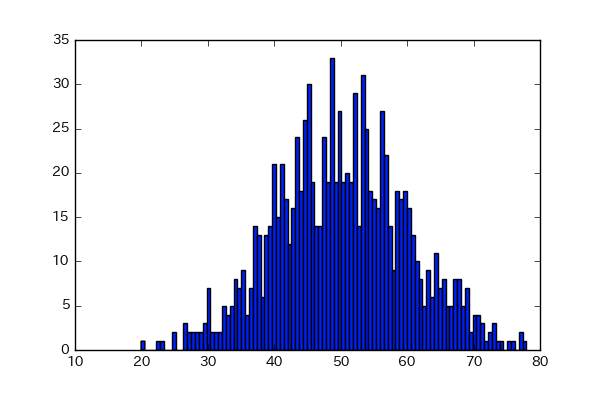Sec4	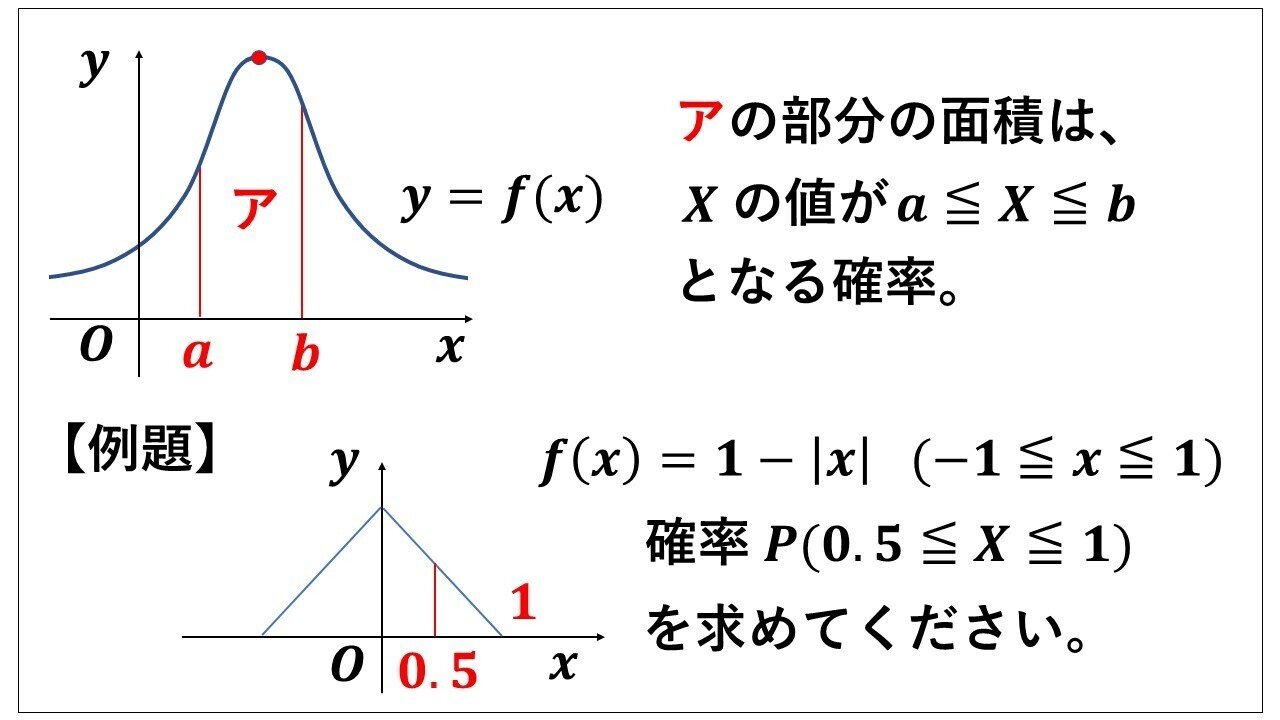Sec4
Sec4	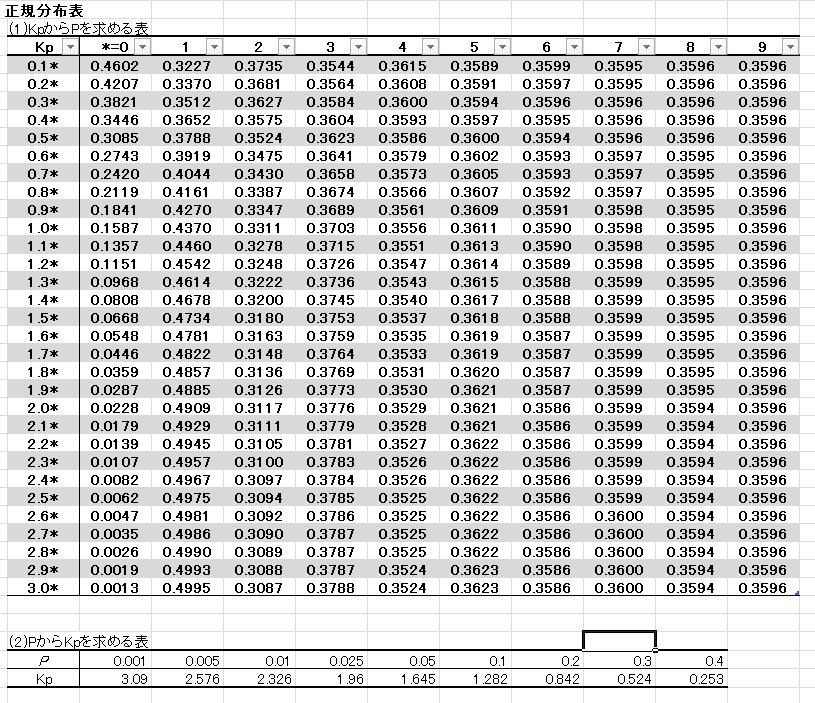Sec4	Sec4
Sec4	Sec4	Sec4
Sec4	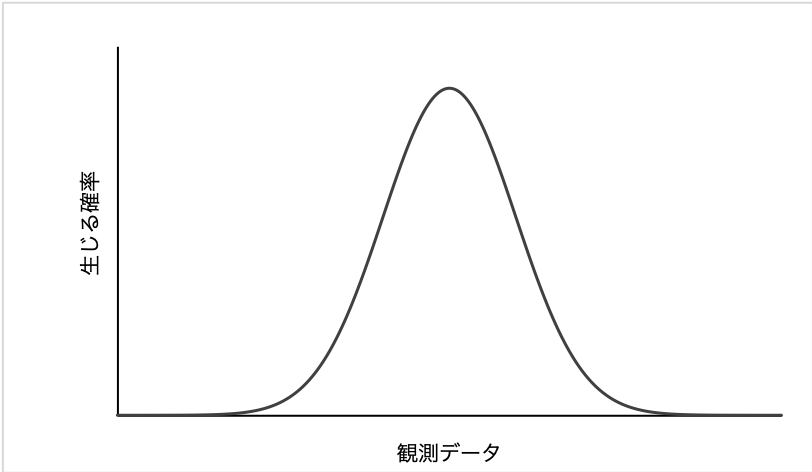Sec4	Sec4
Sec4	Sec4	Sec4
Sec4

 対数正規分布は、 （実数）と （正の定数）という2つのパラメータをつかって表現されます。 ちなみに、上の図で示している対数正規分布の確率密度関数は、以下のようにRで実行することで得られます（ ）（平均と "標準偏差" を指定しているので注意2 二項分布の式を変形し、極限を利用してポアソン分布の公式を得る 21 サンプル数がわからなくても確率の計算が可能;

Incoming Term: 正規分布 確率 例題,